零点定理的一个拓扑学证明

我们高中时都学过一个非常常用的定理，零点定理，或者也叫介值定理(弱化版)。它的内容叙述如下：

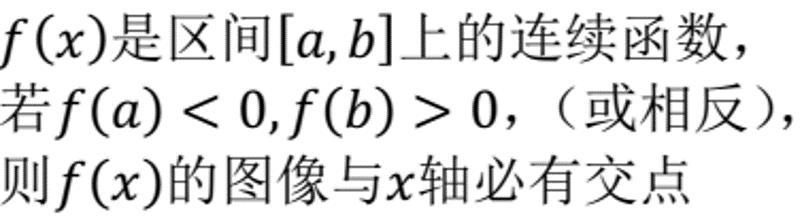
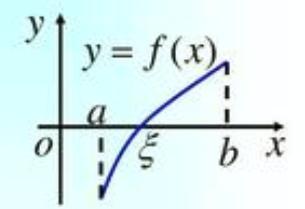
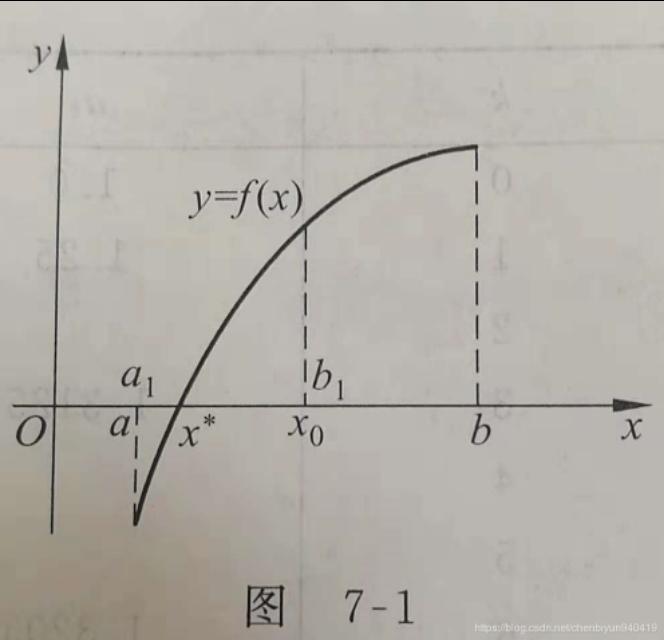
它的图形画出来如下所示

这个定理表面上看起来非常显然，似乎不需要证明。但事实上，数学上任何一个定理，即使看起来再显然，也是需要经过严格证明的。我之前曾写过一篇文章介绍过零点定理的证明，使用的是数学分析中的确界原理。文章链接如下：

一个看似极其显然，证明却极其困难的数学定理

确界原理是实数完备性定理中的一个重要定理，与此同时还有另外五个与之等价的定理，一共六个定理，数学专业的同学会在《数学分析》这门课程里面学的，这六个定理都可以用来证明零点定理，因此我在文章中说，它的证明方法一共有六种。后来有网友评论到，其实可以跳出实数完备性定理的框架，用更高级的数学知识，比如拓扑学来证明。于是我在其启发下，想到了一种用拓扑学的知识来证明该定理的方法，本文就来介绍，欢迎讨论。

当然既然要利用拓扑学的知识，就首先对拓扑学的一些基本概念做一些简要介绍。拓扑学的研究对象非常复杂，但仅就零点定理而言，我们只需要理解一维实数轴上的拓扑空间就足够了，我将用最简单的语言来进行描述。

概念1：开集

设U为实数集的一个子集，如果U满足如下条件：

从U中任取一个数a，都可以找到一个以a为中心的小的开区间(a-δ，a+δ)，使得这个小区间完全包含在U里面。

那么就称U为一个开集。

任何一个开区间都是开集，比如我们拿(0，1)举例子。我在上面任意选一个数，比如0.5，那么(0.4，0.6)是完全包含在(0，1)之间的。选的数离1很近也不要紧，比如0.99，那么(0.989，0.991)是完全包含在(0，1)里的，诸如此类，所以开区间(0，1)就是一个开集。

当然开集不只是包含开区间，任意两个开区间的并集也是开集，比如(0，1)∪(2，3)。

同时，有界闭区间就不是开集了，比如闭区间[0，1]。因为我可以在上面取一个点1，任何一个以1为中心的小的开区间都不能完全包含在[0，1]之内。所以有界闭区间不是开集。

那么闭区间到底是一个什么样的集合呢？这时我们就需要引入闭集的概念。

概念2：闭集

设V为实数集的一个子集，如果它的补集是一个开集，那么称V为一个闭集。

于是很显然，一个有界闭区间就是一个闭集。我们还拿[0，1]举例子，它的补集(-∞，0)∪(1，+∞)是一个开集，因此它是一个闭集。同样道理，两个闭区间的并集也是闭集。

从上面对开集的定义中，我们可以很明显地看出如下定理：

定理：多个开集的并集还是开集

但凡定理都需要证明，这个定理的证明比较容易，我们就拿两个集合举例。假设集合A与集合B都是开集，下面我们来研究A∪B。从A∪B中任取一个元素x，那么x至少在A或B中的一个里面。如果x在A里面，那么因为A是开集，根据开集的定义，我们就可以找到一个以x为中心的小区间(x-δ，x+δ)，使得它完全包含在A里面，A肯定完全包含在A∪B里面，所以(x-δ，x+δ)一定完全包含在A∪B里面。同样道理，如果x在B里面，我们也可以类似证明。所以对于你任意取的一个x，一定可以找到以x为中心的小区间完全包含在A∪B里面，于是A∪B就是一个开集。

开集和闭集是拓扑学中最基本的两个概念，他们在一般的拓扑空间中有着更抽象的定义，但是本文涉及不到。本文介绍的只是在一维实数轴上所对应的开集与闭集的定义，用它我们就可以来证明零点定理了。

我们把问题再具体叙述一下。

f(x)在[a，b]上连续，且f(a)<0，f(b)>0，求证在该区间内必存在一点使得f(x)=0

证明：我们把闭区间[a，b]中所有的数分为三个集合，分别用A，B，C表示：

A = { x∈[a，b] | f(x)<0 }

B = { x∈[a，b] | f(x)>0 }

C = { x∈[a，b] | f(x)=0 }

一个数无非小于0，大于0，等于0三种情况，于是 A∪B∪C = [a，b]。

我们来证明C一定不是空集。这样一来C中至少包含一个元素，这些元素就是f(x)=0的点。

采用反证法：假设C是空集。

于是就只剩下A和B，即 A∪B =[a，b]。

对于集合A，随便选一个点c∈A，则有f(c)>0，因为函数连续，则

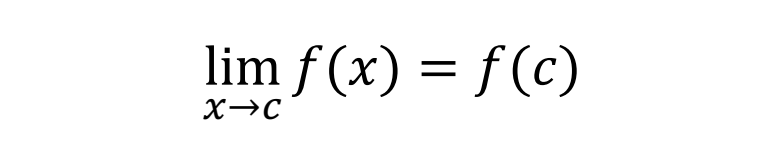
现在已知f(c)>0，因此利用函数极限的保号性，存在某个小区间(c-δ，c+δ)，使得x∈(c-δ，c+δ)时有f(x)>0，也就是这个小区间内所有的数都在满足集合A的条件，也就是说它都在A里面，即(c-δ，c+δ)⊂A，那么根据上面开题的定义，因为这个c是任意选的，所以A一定是一个开集。

同理，利用极限的保号性可以证明集合B也一定是一个开集。

按照我们前面讲过的定理：两个开集的并集也是开集，于是A∪B 也是开集，又因为我们前面按照假设A∪B =[a，b]，因此[a，b]也是开集。

但我们前面经过论证，有界闭区间一定不是开集，于是得到矛盾，假设不成立，即C不是空集。

于是C中包含的数就是使f(x)=0的数，证毕。

用这种方法来证明零点定理，过程相对比较简单，但是理解起来相对困难，因为它使用了拓扑学中开集这个概念。而开集又是依赖于开区间的，这道题的关键是利用极限的保号性构造出一个小的开区间，把这块儿理解了，那么整个过程也就不难理解了。

零点定理在证明方程解的存在性等问题中有着决定性的作用，同时还可以利用它进行方程的求解，比如说二分法，就是利用的零点定理来数值求解方程。

当然，证明零点定理不是只有这一种方法，即使是在拓扑学的框架内，相信也有很多同学能想出其他的方法来。如果有同学有新的方法，可以在评论中提出，欢迎热爱数学的小伙伴们一起来加入讨论！